Research
|
These pages provide non-technical (or at least less-technical) descriptions of my research projects, intended for interested non-experts. I write them both to contribute to public engagement with science and to recognize taxpayer support of my work over the years. Experts may prefer to go directly to my publications. If you have any questions about my work, or comments on this attempt to present it as comprehensibly and correctly as I can, you are welcome to contact me. The essence of my research is to use high-performance computing to gain insight into strongly interacting quantum field theories, through a framework known as lattice field theory. On another page I provide some background on strong dynamics and lattice field theory. Below I summarize various projects I've carried out over the years, some of which are discussed more thoroughly on separate pages. The projects closer to the top of the list are those I'm currently focusing on. For each project I also link my related publications, all of which are freely available online, mostly through the arXiv e-print server. It is important to note that all of this work involves various forms of collaboration, reflected in part by the authorship of those publications. These pages reflect my own views and interests, and I am solely responsible for any errors or omissions. |
 |
Supersymmetric lattice field theories
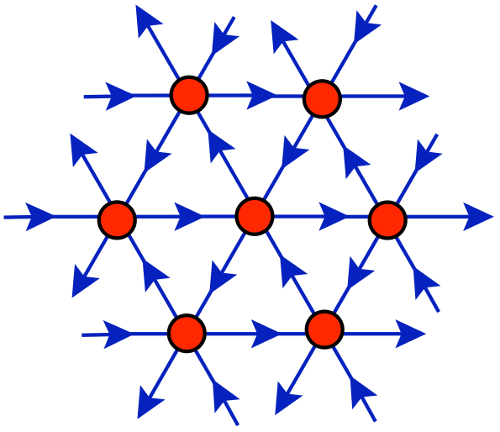 |
While supersymmetry is most famous as a possible extension of the standard model of particle physics, at a more fundamental level it simplifies the systems in question, allowing profound insights into strongly coupled dynamics. These include, for example, the concept of holographic duality between field theories and higher-dimensional gravity. Lattice calculations provide a unique means to analyse supersymmetric field theories from first principles, enabling new tests of such dualities as well as potential new discoveries. Longer discussion Image: The two-dimensional triangular lattice used to define 16-supercharge Yang–Mills theory in discrete space-time, taken from arXiv:0903.4881. Related publications: arXiv:2308.02538, arXiv:2304.04655, arXiv:2303.13880, arXiv:2208.03580, arXiv:2201.08791, arXiv:2201.08626, arXiv:2201.03097, arXiv:2109.01001, arXiv:2102.06775, arXiv:2010.00026, arXiv:2003.01298, arXiv:1904.09964, arXiv:1810.09282, arXiv:1710.06398, arXiv:1709.07025, arXiv:1611.06561, arXiv:1804.07792, arXiv:1512.01137, arXiv:1508.00884, arXiv:1505.03135, arXiv:1411.0166, arXiv:1410.6971, arXiv:1405.0644, arXiv:1309.1206 |
Quantum computing and sign problems
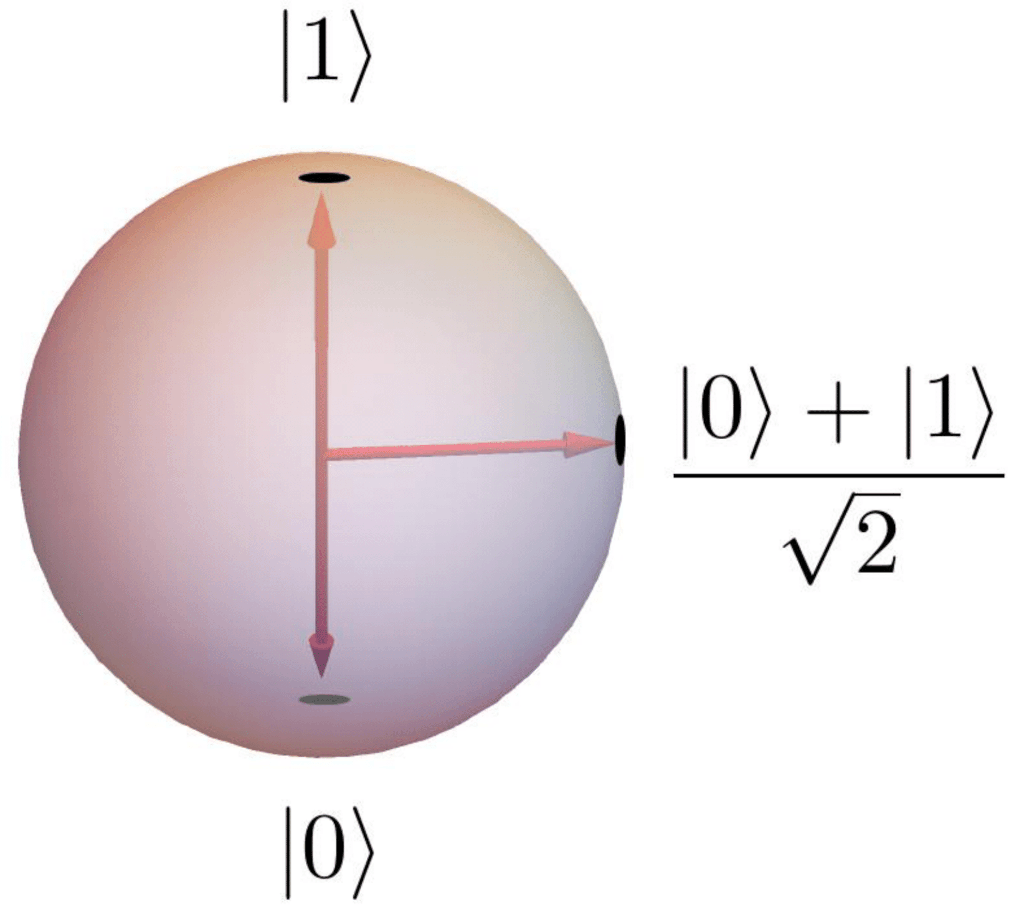 |
A long-standing challenge for lattice field theory is the breakdown of standard importance sampling algorithms when negative or complex numbers appear where these algorithms expect probabilities between 0% and 100%. Such "sign problems" can arise for systems (such as neutron stars) with many more particles than anti-particles, or when considering out-of-equilibrium dynamics. Building on earlier explorations of novel algorithmic approaches designed to reduce the severity of sign problems, I am now applying quantum computing to avoid sign problems entirely. This involves reformulating simple systems in terms of entangled qubits and designing algorithms to simulate them using existing and near-future quantum devices. Image: This visualization of a qubit illustrates how it allows for complex superpositions of the two states 0 and 1. The resulting interference and quantum entanglement between multiple qubits lies at the heart of quantum computing and its promise to go beyond the capabilities of existing computers. Related publications: arXiv:2301.02230, arXiv:2112.07651, arXiv:1712.07585 |
Composite dark matter
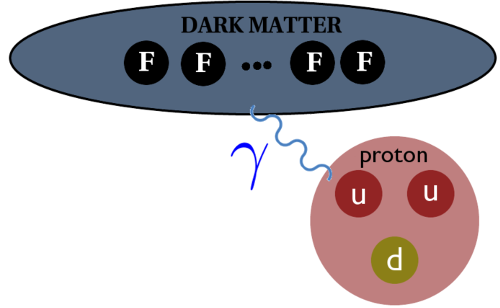 |
It is a remarkable possibility that the dark matter discovered by many different observations of the large-scale universe could consist of composite particles that contain electrically charged constituents. These constituents interact with light but the composite particles they produce are dark, much like electrically charged quarks produce the electrically neutral neutron. Lattice calculations have provided predictions for how such composite dark matter may be seen in ongoing experiments using large underground detectors. Work is in progress to predict additional observable signatures of composite dark matter at high-energy particle colliders and future gravitational wave observatories. Image: A cartoon illustrating dark matter interacting with a proton, by exchanging a photon that couples to the internal structure of the neutral composite dark matter particle. This internal structure is described by electromagnetic form factors, which lattice calculations can determine to predict the rate with which composite dark matter will produce observable signatures in large underground detectors. Related publications: arXiv:2311.10243, arXiv:2303.01149, arXiv:2212.09199, arXiv:2112.11868, arXiv:2006.16429, arXiv:2002.00187, arXiv:1904.09964, arXiv:1503.04205, arXiv:1503.04203, arXiv:1402.6656, arXiv:1309.1206, arXiv:1301.1693 |
Composite Higgs physics and electroweak phenomenology
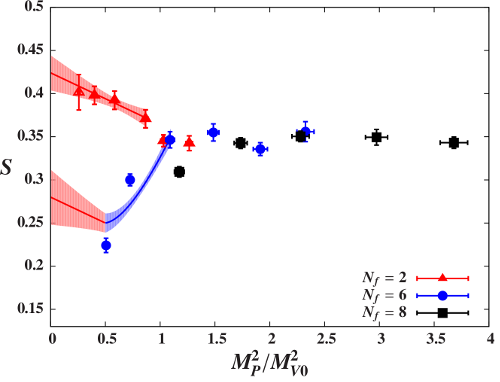 |
The Higgs boson discovered in 2012 may be a composite particle arising from new strong dynamics beyond the standard model, which would explain how it is protected against large quantum corrections. This possibility is currently being investigated by experiments at the Large Hadron Collider, which are imposing increasingly tight phenomenological constraints on composite Higgs models. Using lattice field theory I am obtaining first-principles predictions for the behavior of representative new strong dynamics potentially underlying such models, to be compared against experimental results. Longer discussion Image: The electroweak S parameter for three gauge theories with different numbers of light fermions, from arXiv:1405.4752. Increasing the number of light fermions decreases S in the MP2 → 0 limit relevant for phenomenology. Related publications: arXiv:2306.06095, arXiv:2305.03665, arXiv:2106.13534, arXiv:2007.01810, arXiv:1904.09964, arXiv:1809.02624, arXiv:1807.08411, arXiv:1601.04027, arXiv:1405.4752, arXiv:1310.7006, arXiv:1309.1206, arXiv:1201.3977, arXiv:1111.4993, PhD dissertation, arXiv:1009.5967, arXiv:1002.3777, arXiv:0910.2224 |
Conformal and near-conformal strong dynamics
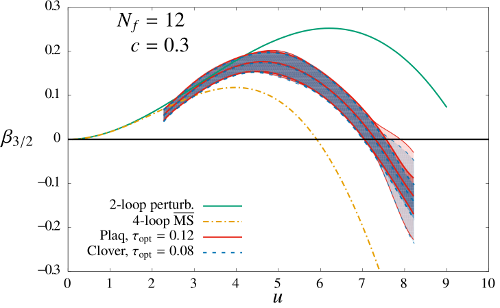 |
The investigations of composite Higgs physics discussed above find that agreement with experimental results improves for theories whose dynamics evolve slowly across a wide range of length scales. This "near-conformal" dynamics is difficult to study through numerical lattice calculations, since only a limited range of length scales can be explored in computations that are practical to run using existing and foreseeable computing hardware. This motivates developing and applying improved lattice techniques to study near-conformal field theories. Image: Lattice results for the step-scaling function β for SU(3) gauge theory with twelve massless fermions, from arXiv:1610.10004. This quantity describes how the interaction strength of the system changes upon moving from higher to lower energy scales. When β crosses zero the system is conformal, identical at all energy scales. Related publications: arXiv:2007.01810, arXiv:1904.09964, arXiv:1610.10004, arXiv:1506.08791, arXiv:1410.5886, arXiv:1404.0984, arXiv:1401.0195, arXiv:1311.4889, arXiv:1311.2679, arXiv:1311.1287, arXiv:1310.1124, arXiv:1309.1206, arXiv:1303.7129, arXiv:1301.1355, arXiv:1212.0053, arXiv:1207.7164, arXiv:1207.7162, arXiv:1204.6000, arXiv:1111.2317, arXiv:1106.2148 |
Topological phases and topological phase transitions
 |
Phase transitions typically separate a phase with a broken symmetry from a different phase in which that symmetry is preserved, allowing the phases to be distinguished by a local order parameter. More recently transitions have been discovered between distinct phases with the same symmetries, which are instead distinguished by non-local "topological" properties. The importance of these topological phase transitions was recognized by the 2016 Nobel Prize in Physics. My work in this area investigates simple lattice field theories that may exhibit topological phase transitions, in particular considering a mechanism to generate particle masses without breaking any symmetries. Image: A signal of a phase transition in a simple lattice field theory that involves four-fermion interactions, from arXiv:1810.06117. Although the symmetries of the system are the same in both phases on either side of the transition, the fermions are massive for large four-fermion coupling G but massless for small G. Related publications: arXiv:2002.00034, arXiv:1810.06117, arXiv:1710.08137, arXiv:1609.08541 |
Strange quark content of the nucleon
 |
Quantum fluctuations in the strange-quark field affect the properties of composite particles even when the quantum numbers of those composite particles don't depend on strange quarks. I have used lattice QCD to investigate strange-quark contributions both to the mass and to the internal structure of nucleons (protons and neutrons). This requires challenging computations of quark-line-disconnected diagrams. Longer discussion Image: Schematic diagram illustrating a quark-line-disconnected diagram that contributes to the electromagnetic form factors governing how nucleons (N) interact with photons (γ). Related publications: Lat12:166, arXiv:1012.0562 |
Graphene
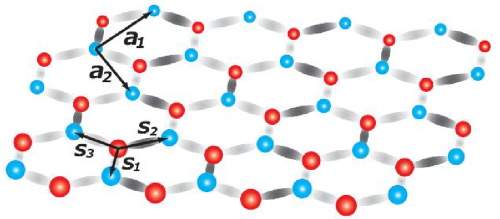 |
The 2010 Nobel Prize in Physics was awarded to recognize the experimental isolation and characterization of graphene, a remarkable two-dimensional material consisting of carbon atoms arranged in a regular honeycomb lattice. Among the many unusual properties of graphene, in the context of lattice field theory the existence of strongly interacting massless fermion quasi-particles is particularly significant. My work on graphene focused on showing how lattice field theory can be applied to study this material non-perturbatively from first principles. Image: A picture showing the layout of carbon atoms in the two-dimensional graphene system, taken from 2015 Aspen lectures by Igor Herbut. The colors show the two triangular sub-lattices of graphene: Atoms colored red have three nearest-neighbor atoms colored blue (and vice versa), and are farther away from any other atoms colored red. Related publications: arXiv:1204.5424, arXiv:1101.5131 |
Algorithm development
 |
There are many algorithmic challenges to address in lattice field theory research, which can significantly impact which physics questions can be answered in a reasonable amount of time. The progress of the field depends on both developing improved numerical algorithms and implementing them efficiently on cutting-edge hardware. In addition to the algorithm development I carried out for many of the physics-focused projects listed above, I have also worked on lattice fermion formulations with improved chiral symmetry as well as the issue of critical slowing down. In some cases it is best to explore these challenges in simpler test systems, which can provide excellent opportunities for beginners to quickly contribute to the field. Image: From arXiv:1403.2761, correlated predictions for the topological susceptibility and (inverse) auto-correlations of lattice QCD calculations, obtained from a novel maximum-likelihood analysis of transitions between topological sectors. Related publications: arXiv:1403.2761, arXiv:0906.2813, arXiv:0902.0045, Bachelor thesis |
Last modified 27 November 2023


