Research — Supersymmetric lattice field theories
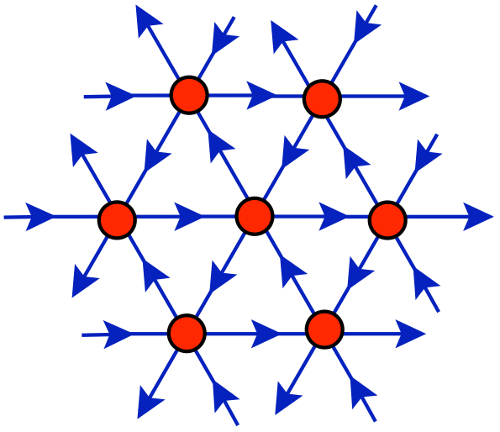 |
Summary: While supersymmetry is most famous as a possible extension of the standard model of particle physics, at a more fundamental level it simplifies the systems in question, allowing profound insights into strongly coupled dynamics. These include, for example, the concept of holographic duality between field theories and higher-dimensional gravity. Lattice calculations provide a unique means to analyse supersymmetric field theories from first principles, enabling new tests of such dualities as well as potential new discoveries. Image: The two-dimensional triangular lattice used to define 16-supercharge Yang–Mills theory in discrete space-time, taken from arXiv:0903.4881. Related publications: arXiv:2308.02538, arXiv:2304.04655, arXiv:2303.13880, arXiv:2208.03580, arXiv:2201.08791, arXiv:2201.08626, arXiv:2201.03097, arXiv:2109.01001, arXiv:2102.06775, arXiv:2010.00026, arXiv:2003.01298, arXiv:1904.09964, arXiv:1810.09282, arXiv:1710.06398, arXiv:1709.07025, arXiv:1611.06561, arXiv:1804.07792, arXiv:1512.01137, arXiv:1508.00884, arXiv:1505.03135, arXiv:1411.0166, arXiv:1410.6971, arXiv:1405.0644, arXiv:1309.1206 |
Supersymmetry is a hypothesized extension of the known symmetries of space-time, which provides one of the most promising potential explanations of how the Higgs boson discovered in 2012 may be protected against large quantum corrections. (Another prominent possibility is that the Higgs boson may be a composite particle, another primary focus of my research.) In practice, supersymmetric extensions of the standard model of particle physics cancel quantum corrections from fermions by introducing new bosonic super-partner particles, and vice versa. Some of these new particles could even serve as the dark matter of the universe, which so far has been observed only through its gravitational effects. Supersymmetry also attracts interest as an ingredient of string theory, a framework that currently provides a promising path towards an understanding of quantum gravity.
At a more fundamental level supersymmetry—like all symmetries in physics—simplifies the systems under consideration. This has led to profound insights into strongly coupled dynamics, in particular the exploration of dualities, subtle phenomena in which apparently unrelated theories describe identical physics. These include both electric–magnetic dualities connecting pairs of supersymmetric quantum field theories (QFTs) with different gauge groups and matter content, as well as the even more remarkable holographic dualities between d-dimensional QFTs and supersymmetric gravity (string theories) in d+1 space-time dimensions.
In general these dualities are conjectured and then subjected to non-trivial consistency checks carried out in special regimes where the systems simplify further. In principle lattice calculations provide a unique means to analyse supersymmetric QFTs in strongly coupled regimes where other approaches are inapplicable, enabling novel tests of such dualities as well as potential new discoveries. In practice, however, lattice investigations of supersymmetric systems are complicated by the nature of supersymmetry as an extension of continuous space-time symmetries: Products of two supercharges (generators of supersymmetry transformations) produce infinitesimal space-time translations, which do not exist in the discrete space-time of the lattice. This explicitly breaks supersymmetry at the classical level, causing quantum corrections to introduce supersymmetry-violating effects into the lattice calculations (e.g., non-zero masses for fermionic and scalar super-partners of the massless gauge field), which must be removed by fine-tuning the bare input parameters. While such fine-tuning can be done, in general it makes numerical calculations prohibitively expensive.
In recent years this obstruction has been overcome for certain supersymmetric QFTs, including d-dimensional SYM theories with at least Q = 2d supercharges. The breakthrough is a clever change of variables (known as topological twisting) that identifies at most Q / 2d ≥ 1 linear combinations of the supercharges that square to zero—effectively producing 'infinitesimal translations' that cycle back around to their starting point. This subset of the supercharges can be preserved exactly in discrete space-time, which protects the lattice calculations from supersymmetry-violating quantum corrections and guarantees the recovery of the correct continuum limit with little to no fine-tuning.
I have taken advantage of this recent progress to initiate large-scale lattice investigations of maximally supersymmetric Yang–Mills theory (N=4 SYM) in 3+1 space-time dimensions. N=4 SYM is a particularly important super-conformal gauge theory that possesses the maximal Q=16=24 supercharges, a high degree of symmetry that makes it arguably the simplest non-trivial QFT in d=4 dimensions. These symmetries force the theory to depend only on the 't Hooft coupling λ = g2N and the number of `colours' in its SU(N) gauge group. The only field content consistent with the symmetries is a single super-multiplet containing the gauge field, four fermions and six scalars, all of which must be massless and transform in the adjoint representation of the gauge group. This simplicity makes N=4 SYM an ideal testbed for theoretical explorations, which led to breakthrough discoveries of both electric magnetic and holographic dualities.
By developing new high-performance parallel software (released under an open-source free software license), I have been able to compute key quantities characterizing N=4 SYM, including the static potential Coulomb coefficient and conformal operator scaling dimensions as functions of the 't Hooft coupling. Holographic duality makes predictions for both of these quantities in the planar regime N, λ → ∞ with λ ≪ N, while lattice calculations are most tractable for smaller values of N. My current results, for λ ≲ 2 and N ≤ 4, appear compatible with perturbation theory, and I am now exploring stronger couplings and larger N to search for the approach to the holographic regime.
At the same time, I have begun investigating the reduction of N=4 SYM to lower dimensions, considering in particular maximally supersymmetric Yang–Mills (with Q=16) in two and three space-time dimensions. Using the same topologically twisted approach described above, I have explored the thermodynamics of these theories, which conjectured holographic dualities relate to properties of certain black hole and black brane solutions in string theory. I am now working on adding matter super-multiplets (analogs of quarks and squarks) to the two-dimensional system, realizing a form of supersymmetric quantum chromodynamics (SQCD) on the lattice. In addition to enabling investigations of phenomena such as dynamical supersymmetry breaking, this work on two-dimensional SQCD will serve as a first step towards the more challenging realization of lattice SQCD in three and four space-time dimensions.
Last modified 27 November 2023


