Research — Composite Higgs physics and electroweak phenomenology
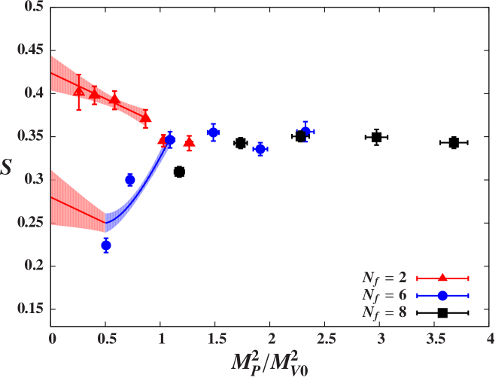 |
Summary: The Higgs boson discovered in 2012 may be a composite particle arising from new strong dynamics beyond the standard model, which would explain how it is protected against large quantum corrections. This possibility is currently being investigated by experiments at the Large Hadron Collider, which are imposing increasingly tight phenomenological constraints on composite Higgs models. Using lattice gauge theory I am obtaining first-principles predictions for the behavior of representative new strong dynamics potentially underlying such models, to be compared against experimental results. Image: The electroweak S parameter for three gauge theories with different numbers of light fermions, from arXiv:1405.4752. Increasing the number of light fermions decreases S in the MP2 → 0 limit relevant for phenomenology. Related publications: arXiv:2306.06095, arXiv:2305.03665, arXiv:2106.13534, arXiv:2007.01810, arXiv:1904.09964, arXiv:1809.02624, arXiv:1807.08411, arXiv:1601.04027, arXiv:1405.4752, arXiv:1310.7006, arXiv:1309.1206, arXiv:1201.3977, arXiv:1111.4993, PhD dissertation, arXiv:1009.5967, arXiv:1002.3777, arXiv:0910.2224 |
While the energy of strong quantum chromodynamics (QCD) interactions is responsible for the vast majority of the mass of composite particles (as discussed here), a small fraction comes from the masses of elementary particles such as the quarks and electrons highlighted in the picture below. The elementary particles are those that do not yet exhibit any signs of substructure, with experiments determining that their maximum possible size must be smaller than roughly a billionth of a nanometer (an attometer, 10-18 m).
The non-zero masses of elementary particles were a key clue that helped drive the development of the standard model of particle physics. The "electroweak" unification of electromagnetism and the weak nuclear force, proposed in the early 1960s, naively appeared incompatible with the existence of massive elementary particles. This obstacle was overcome in the mid-to-late 1960s with the realization that the electroweak symmetry can be hidden (or "spontaneously broken"). This process is now known as the Higgs mechanism, and is a core component of the standard model. The basic features of the standard model were clearly confirmed by decades of experiments leading up to the 2012 discovery of a standard-model-like Higgs boson by experiments at the Large Hadron Collider at CERN, the European Organization for Nuclear Research.
A key question for the future development of particle physics is whether the Higgs boson is itself an elementary particle, or arises from some new strong dynamics with a characteristic distance scale roughly 10,000 times smaller than the femtometer (10-15 m) scale of QCD discussed on the background page. Because this new interaction is strong, lattice field theory is needed to quantitatively predict its features and the properties of the resulting composite Higgs boson.
Much of my work in this area has been carried out with the Lattice Strong Dynamics Collaboration. Our goal is to learn what range of phenomena are possible in strongly coupled quantum field theories, with specific applications to the physics of composite Higgs models and composite dark matter.
For example, the plot at the top of this page shows some of my results for an important "precision electroweak observable" known as the S parameter. This quantity parameterizes the impact that the physics underlying the Higgs mechanism has on several electroweak observables (such as the mass of the W boson, decays of the Z boson, and atomic parity violation in heavy elements such as cesium) that can be measured very precisely. Those experimental measurements lead to a small value S = 0.03 ± 0.10, consistent with zero, which powerfully constrains possible theories of new strong dynamics.
If we assume that QCD-like new strong dynamics is responsible for the Higgs mechanism, we would expect S > 0.4, in considerable disagreement with experiment. This corresponds to the red points in the plot at the top of this page, which I calculated using lattice QCD with two light fermions. The blue and black points come from my investigations of theories with three and four times as many light fermions, respectively. These results show that increasing the number of light fermions decreases S in the MP2 → 0 limit relevant for phenomenology, moving it closer to the experimental value.
Last modified 17 July 2023


