Research — Background: Strong dynamics and lattice field theory
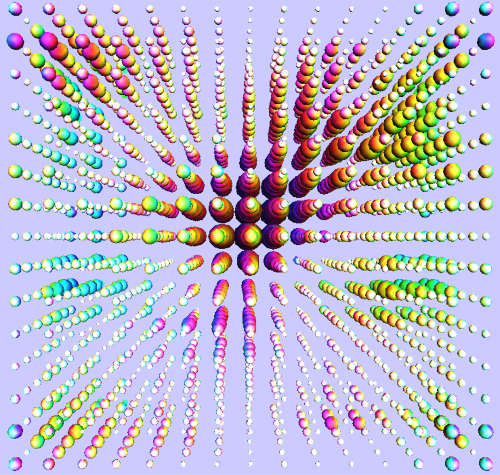 |
Summary: The essence of my research is to use high-performance computing to gain insight into strongly interacting quantum field theories, through a framework known as lattice field theory. Here I provide some non-technical background on strong dynamics and lattice field theory. Image: A snapshot, produced by Claudio Rebbi, of a quantum field configuration in a discretized lattice space-time (which was used to compute properties of protons). The snapshot shows the three spatial dimensions of the lattice at a particular time. The colors represent the "color" charges of quarks governed by the theory of quantum chromodynamics and the size of each sphere shows the magnitude of the color field at the corresponding point in space. |
Quantum field theory (QFT) is a fundamental principle that underlies much of modern particle, nuclear and condensed-matter physics. I can't explain QFT in a quick, non-technical way. I had to take multiple graduate courses on the subject in order to earn my PhD, and I still learn more about QFT every day as I work on the cutting edge of physics research. I can, however, summarize some pertinent information. To learn more about QFT (and many other subjects) Wikipedia is a good place to start—but a terrible place to stop.
Qualitatively, QFT is what we get upon combining quantum mechanics with special relativity. The quantum mechanics part of the recipe allows systems with the same characteristics (the same quantum numbers) to transform into one another, or even coexist as an unresolved superposition. Special relativity, through its famous formula E = mc2, allows various forms of energy (e.g., kinetic energy) to be transformed into mass and vice versa. Relativity also connects space and time, combining them into a single (3+1)-dimensional space-time. In the end QFT describes relativistic quantum fields filling every point in space-time. Particles correspond to ripples in these quantum fields. In addition, the quantum fields also fluctuate in more general ways that don't behave like particles.
A certain class of QFTs known as gauge theories are particularly important. For example, the standard model of particle physics is a gauge theory, as is the more familiar electromagnetism that it contains. The terminology refers to a feature of these theories that allows the fields to be transformed into different "gauges" at each point of space-time without changing any physical predictions.
While this brief introduction is obviously very fuzzy, the mathematics of QFT is not. Extraordinarily precise physical predictions result from QFT calculations, which involve integrating over all possible values of all relevant fields at every space-time point. Since space-time appears to be continuous, with infinitely many distinguishable times and locations, we end up having to compute infinite-dimensional integrals, where the mathematical "dimensions" of the integral correspond to the independent degrees of freedom in the system (as opposed to the 3+1 dimensions of space-time). This is difficult.
The simplest QFT analyses follow an approach known as perturbation theory. This is a procedure that begins by considering simple systems in which the quantum fields don't interact with each other at all. It then attempts to incorporate the effects of interactions by treating them as small corrections (perturbations) to the simple starting system. This works when those interactions are weak in strength.
Things can become much more difficult when strong interactions are involved. The most familiar strongly interacting QFT is quantum chromodynamics (QCD), the "color" theory of the strong nuclear force that binds quarks and gluons into composite particles such as protons. To understand why we say this interaction is "strong", imagine pulling apart two quarks: separating them by a femtometer (10-15 m, one millionth of a nanometer) would require a force of roughly 10 tons to balance the attractive color force pulling the quarks together. That's strong.
Lattice field theory is a framework that allows us to study strongly interacting QFTs without relying on perturbative approximations. Instead we make a different kind of approximation by replacing continuous space-time with a regular, finite grid of discrete points connected by links—the lattice. The fields involved in the theory are likewise discretized, and defined on the lattice in such a way that we recover the original system in the continuum limit where the lattice possesses infinitely many points infinitesimally close together. I mostly work on lattice gauge theory, which applies this procedure to the gauge field theories mentioned above. While lattice techniques are best known in the context of lattice QCD, my research emphasizes that lattice field theory is a broadly applicable tool with which we can investigate a much wider variety of strongly interacting systems.
Now that the systems we're considering have a finite number of degrees of freedom, the integrals that we need to compute have a finite number of dimensions. For example, the largest systems I've studied involve roughly billion-dimensional integrals. With some effort, we can evaluate these integrals numerically using finite computers, thereby obtaining quantitative predictions for strongly interacting QFTs without relying on perturbative approximations or other simplifications (like the large-N planar limit mentioned elsewhere on this site) that are required to carry out pen-and-paper calculations.
It should go without saying that these numerical calculations are not easy—a billion dimensions are still a lot, and in general we're interested in getting as close to the continuum limit as we can, to ensure that the discretization of space-time (our trick for simplifying the QFT calculation) doesn't introduce any noticeable artifacts in our predictions. For decades the lattice field theory community has helped to drive advances in high-performance computing, simultaneously deploying large-scale parallel codes across thousands of cores in the world's biggest supercomputers as well as developing advanced algorithms to get the most benefit out of this investment in computer time.
The central numerical technique we employ is known as importance sampling Monte Carlo. This approach takes advantage of the fact that almost all of the field configurations over which we need to integrate are actually irrelevant—they contribute negligible decimal dust to the final answer. In order to make the computation efficient, we design and use sophisticated algorithms to determine (on the fly) which field configurations are the most important for the system being studied, and then ignore all the rest. These numerical methods use (psuedo)random numbers to find the important field configurations to sample, which led to the "Monte Carlo" terminology. Depending on how many degrees of freedom there are in the system, and how much computing time we have to devote to it, we will typically evaluate integrals using only a few dozen or a few hundred independent configurations. This leaves statistical uncertainties on the resulting predictions, which can be improved by investing more computing time.
In addition to applying lattice field theory to study various strongly coupled systems within and beyond the standard model of particle physics, the research projects described in the other pages also investigate the underlying numerical methods, continuously improving them in order to obtain the best results from the available computing resources.
Last modified 5 April 2022


