Research — Algorithm development
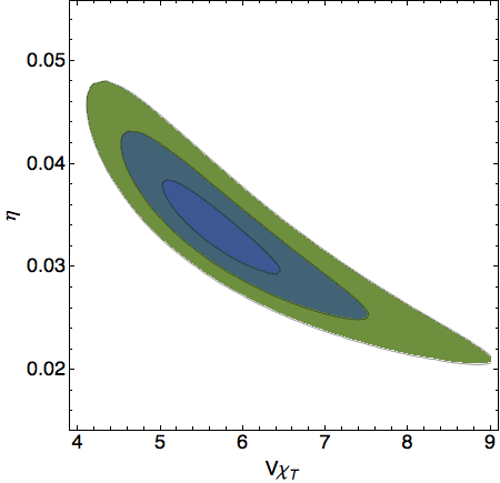 |
Summary: There are many algorithmic challenges to address in lattice field theory research, which can significantly impact which physics questions can be answered in a reasonable amount of time. The progress of the field depends on both developing improved numerical algorithms and implementing them efficiently on cutting-edge hardware. In addition to the algorithm development I carried out for many of the physics-focused projects listed above, I have also worked on lattice fermion formulations with improved chiral symmetry as well as the issue of critical slowing down. In some cases it is best to explore these challenges in simpler test systems, which can provide excellent opportunities for beginners to quickly contribute to the field. Image: From arXiv:1403.2761, correlated predictions for the topological susceptibility and (inverse) auto-correlations of lattice QCD calculations, obtained from a novel maximum-likelihood analysis of transitions between topological sectors. Related publications: arXiv:1403.2761, arXiv:0906.2813, arXiv:0902.0045, Bachelor thesis |
My research relies on steady advances in numerical algorithms complementing improvements in computing hardware.
A basic ingredient of lattice calculations is repeated solution of a linear system, Ax=b, where A is a large sparse matrix. "Large" means that this matrix has millions of rows and millions of columns, involving far too much information to store in a computer's memory. "Sparse" means that most of its elements are exactly zero. Even storing only the relatively few non-zero matrix elements is outrageously inefficient. Instead, we use iterative methods such as the conjugate gradient algorithm to solve this equation for x without explicitly allocating memory for the full matrix A.
I have performed research into the development of improved lattice fermion formulations with algorithms, . A final interesting aspect of this line of research is that it can provide an entry point into the field. We often use simple models to design and test improved techniques. These smaller-scale computational projects can be more tractable for beginners, while still providing significant benefits to the field as a whole.
Last modified 18 March 2019


