Research — Strange quark content of the nucleon
 |
Summary: Quantum fluctuations in the strange-quark field affect the properties of composite particles even when the quantum numbers of those composite particles don't depend on strange quarks. I have used lattice QCD to investigate strange-quark contributions both to the mass and to the internal structure of nucleons (protons and neutrons). This requires challenging computations of quark-line-disconnected diagrams. Image: Schematic diagram illustrating a quark-line-disconnected diagram that contributes to the electromagnetic form factors governing how nucleons (N) interact with photons (γ). Related publications: Lat12:166, arXiv:1012.0562 |
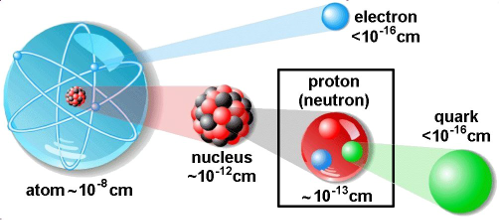
As the fundamental theory of the strong nuclear force, quantum chromodynamics (QCD) is responsible for quarks being confined into composite particles such as nucleons (protons and neutrons), through the quarks' interactions with gluons. The picture below illustrates where quarks and nucleons fit into the structure of matter, but it's not the whole story: While it shows a nucleon consisting of three quarks, the nucleon's mass is roughly 100 times larger than the mass of those three quarks. The vast majority of the mass of composite particles—and thus of the visible universe—comes from the energy of strong QCD interactions.
The lattice regularization of QCD was formulated in the 1970s, with numerical calculations beginning in the 1980s. The field has advanced steadily since then, in parallel with the development of high-performance computing. Among many other achievements, lattice QCD calculations are now able to predict the mass of the nucleon from first principles with percent-level accuracy, the culmination of decades of progress.
In many ways, predicting the mass of the proton is a relatively easy calculation in the framework of lattice QCD. My own work on QCD focused on studying the strange quark content of nucleons. Although strange quarks are not among the "valence" quarks that determine the quantum numbers of the nucleons, the energy of the strong interaction allows pairs of strange quarks and antiquarks to be continually produced and annihilated through quantum processes. These "virtual" strange quark pairs account for a portion of the nucleon's mass, and affect its internal structure.
The fact that only pairs of strange quark and antiquarks appear in the nucleon means that their contributions to its properties arise through closed loops like that shown in the image at the top of this page In order to evaluate such quark-line-disconnected diagrams exactly, the computation must be repeated with the closed loop of strange quarks located at every possible point in space and time—that is, at every site on the lattice. Since typical lattices include millions of sites, this is not computationally feasible. Instead we employ stochastic methods to probabilistically estimate the result. This still requires much more computing than does evaluating connected diagrams, and introduces a new source of statistical noise.
Last modified 18 March 2019


